Fractal Flames

Fractal Flames are an extension of Iterated Function Systems. In order to understand how the Fractal Flame algorithm works, it is useful to first understand Iterated Function Systems. The term "Iterated Function System" refers both to a mathematical object and a method used to generate fractals from these objects.

Without going into too much detail, an Iterated Function System (IFS) is a finite set of contraction mappings on a metric space.

A metric space is a set which has a notion of distance, called a metric, which is a function that takes two members of the set and gives a measure of the distance between them, which is some real number. A common example of a metric space is the Euclidean plane, which has the common distance metric (technically known as the Euclidean distance, or the "$L^2$" norm)

For more information on metric spaces, check out the Wikipedia article on the subject.

There is similarly an intuitive notion of the concept of a contraction mapping. A contraction mapping on a metric space $X$ is simply a function that takes elements of $X$ and outputs elements of $X$ that are closer together (acording to the metric) than the original elements. A good example of this would be a function that maps each coordinate of any point on the Euclidean plane to $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ of its value, halving its distance from the origin.

Again, for more information, check out the Wikipedia article on contraction mappings.

An important property of Iterated Function Systems (actually, the property we care most about) is that, (according to Shannon) for any IFS, the union of the images under the contraction mappings of the IFS of the set of all compact subsets of the metric space on which the IFS is defined is itself a contraction mapping.

We can understand this symbolically with the Hutchinson operator. The Hutchinson operator is the function $F:H\left(X\right)\to H\left(X\right)$ using the contraction mappings $f_i$ given by

$$F\left(A\right)=\bigcup _{i=1}^N{f}_i\left(A\right)$$

where $H\left(X\right)$ is the set of nonempty compact subsets of $X$.

The important thing about this operator is that it is what guarantees that Iterated Function Systems have what is known as attractors, sets of points that each IFS will tend toward when the method of Iterated Function Systems is applied.

For more information on why this works, see Shannon's article Fractals, Image Compression and the Contraction Mapping Theorem.

The name "Iterated Function System" comes from the way in which the mathematical objects called "Iterated Function Systems" are used. Essentially, the functions (contraction mappings) in an IFS describe a way to transform an image to produce a new image. When these functions are applied repeatedly (iterated), the result tends to be the self-similar images we know as fractals.

Simple Iterated Function Systems with just one or two functions are easy to understand, and many (such as an IFS describing the Cantor ternary set) can be used to construct fractals by hand with ease. Eric Green of University of Wisconsin-Madison has an introduction to constructing fractals using this method, complete with several demonstrations of the principle of the IFS method

Despite the fact that the IFS method is reliable and straightforward, the method is very inefficient when compared to another method known as the "Chaos Game"

The Chaos Game is a method for generating fractals produced by Iterated Function Systems that uses a stochastic (that is, not deterministic) sampling method. In other words, the Chaos Game is liable to give you different results each time you use the method to generate the same fractal.

Why use a method that would give you a different result each time? In order to understand this, you first need to know how the algorithm works. Simply put, the steps of the Chaos Game are as follows:

1. Pick a random point in the metric space of the IFS. Call this point $p$.
2. Pick a random function from the IFS. Call this function $f$.
3. Apply $f$ to $p$. Set $p$ to $f\left(p\right)$.
4. Go to the second step.

Clearly, this process could last indefinitely, but, of course, it must be stopped at some point in practice.

Remember that the Hutchinson operator guarantees that all Iterated Function Systems converge to their attractors. If $A$ is the attractor of an IFS, then the randomly selected point in the Chaos game may or may not have been in $A$. When we do the steps of the Chaos Game an infinite number of times, we are bound to try all points in any finite set of points. The key is that the Hutchinson operator also guarantees (since it is a contraction mapping) that, if a point $p$ is in $A$, then, for any $f_i$ in the IFS, $f_i\left(p\right)$ is also in the attractor. Since we try all points, we will eventually try a point in $A$, and, so, we eventually "hone in" on the attractor no matter what point we choose as our first $p$. More than this, Draves and Reckase tell us that this statistically happens after only about twenty points.

This is why it makes sense to use a stochastic sampling method for generating an IFS fractal. Although it may not be perfect, it is typically a good tradeoff given the amount of speed gained in using the Chaos Game over the IFS method.

In the demonstration below, you can see the Chaos Game in action producing a fractal. Hold the up arrow on the spinner to generate more points. The red point on the canvas represents the last point generated.

If you're curious, the fractal is generated using the rule that the next point to be drawn is calculated by halving the distance between the last point and a random one of the vertices of a (invisible) square that surrounds the fractal. However, the same vertex of the square can not be picked twice in a row.

Coming soon.

The following are some examples of variations used in the Fractal Flame algorithm

Variation	Definition	Sample Image
Linear	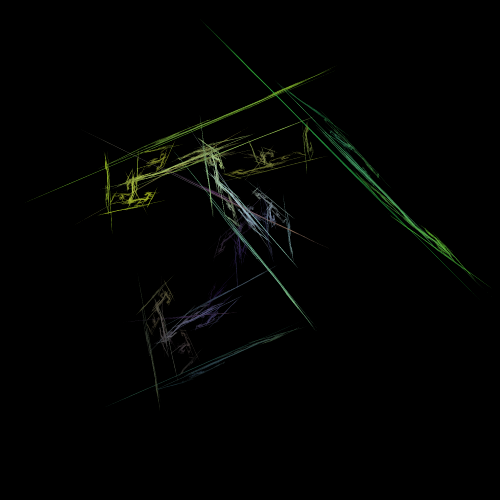$V\left(x,y\right)=(x,y)$
Sinusoidal	$V\left(x,y\right)=(\sin \left(x\right),\sin \left(y\right))$
Spherical	$V\left(x,y\right)=(\frac{\mathrm{x}}{x^2+y^2},\frac{\mathrm{y}}{x^2+y^2})$
Horseshoe	$V\left(x,y\right)=\left(\frac{\left(\mathrm{x}-\mathrm{y}\right)\left(\mathrm{x}+\mathrm{y}\right)}{\sqrt{x^2+y^2}},\frac{2\mathrm{x}\mathrm{y}}{\sqrt{x^2+y^2}}\right)$
Popcorn	$V\left(x,y\right)=\left(x+c\sin \left(\tan \left(3y\right)\right),\mathrm{y}+\mathrm{k}\sin \left(\tan \left(3x\right)\right)\right)$
Eyefish	$V\left(x,y\right)=\left(\frac{2x}{r+1},\frac{2\mathrm{y}}{r+1}\right)$

Coming soon.

Coming soon.

Coming soon.

Coming soon.